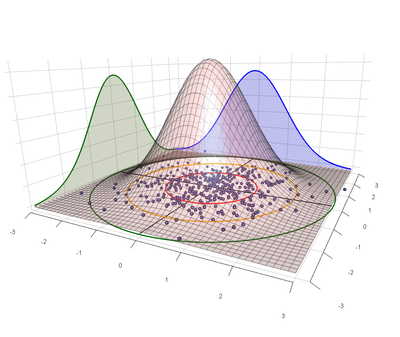
# The assumption of normality ## Multivariate normality In case of multiple dependent variables, multivariate normality is assumed. This means that DV1 (green) and DV2 (blue) are normally distributed individually, AND the linear combination (pink) of DV1 and DV2 is normally distributed as well.  # Homogeneity of variance ## Homogeneity of covariance It is assumed that the [[Variance | variance]] within the dependent variable is equal for each level of the independent variable, for every dependent variable. AND the covariance is similar for every level of the independent variable. Covariance is the joint variance of two dependent variables. The following matrix is the result for three dependent variables (DV) | | DV1 | DV2 | DV3 | |---|---|---|---| | **DV1** | Var(1) | COV(1,2) | COV(1,3)| | **DV2** | COV(1,2) | Var(2) | COV(2,3) | | **DV3** | COV(1,3) | COV(2,3) | Var(3) | *Var. = variance, COV = covariance * >*For example:* > You're assessing the effect of gender (men vs women) on general fitness, which is operationalized by 60m sprint performance (60m), countermovement jump height (CMJ) and a cooper-test (CP). > It is assumed that the variance in 60m_women, CMJ_women, CP_women, 60m_men, CMJ_men and CP_men are similar. > Moreover, the variance shared between 60m_women and CMJ_women, should be similar to the the variance shared between 60m_men, CMJ_men. This also applies to the variance shared between 60m and CP, and CMJ and CP. The variance shared is the covariance. # Homogeneity of regression slopes In case of an [[ANCOVA|ANCOVA]] it is assumed that the relationship, or slope, between the covariate and the dependent variable is similar for every level of the independent variable. # Homoscedasticity In linear models (regressions), it is assumed that the variance of the errors in the model is constant, meaning, that the error of one variable does not depend on the value of the other variable(s). Heteroscedasticity can be understood as an unequal level of residuals for different levels of the dependent variable. This would violate one main assumption of the linear regression model that the residuals do not depend on the level of the DV. ## Example > Heteroscedasticity can be tested using the Breusch-Pagan Test from the package *lmtest*: > **R output** > ![[Breusch-Pagan Test.png]] > Alternatively, White's test can be conducted which tests homoscedasticity also for the squared DV's > **R output** > ![[Whites Test.png]] If the result is significant, we must accept that there is heteroscedasticity within the data. Common solutions to this problems are 1. transform the DV (not recommended as this may lead to violations of other assumptions, especially normality) 2. calculate weighted regressions by calculating the weights for each data point based on the variance of its fitted value. # Independence ## Independence of the covariate In case of an ANCOVA it is assumed that the covariate and the independent variable are independent from each other. In other words, variance explained by the independent variable and variance explained by the covariate in the dependent variable should not overlap. --- --- ---